 ガジェット
ガジェット
【PC初心者】ベンチマークテスト:PassMark(パスマーク)を使ってみよう【PC選び – 備忘録 #8】
 ガジェット
ガジェット  基本情報技術者試験
基本情報技術者試験  Excel
Excel  PowerPoint
PowerPoint  AZ900
AZ900  Excel
Excel  基本情報技術者試験
基本情報技術者試験  ガジェット
ガジェット  IT系知識
IT系知識  IT系知識
IT系知識 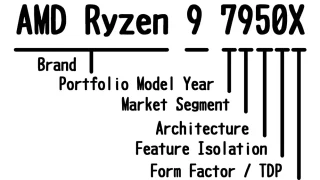 ガジェット
ガジェット  Excel
Excel  Excel
Excel  Java
Java  基本情報技術者試験
基本情報技術者試験  Java
Java  基本情報技術者試験
基本情報技術者試験  PowerPoint
PowerPoint  IoT
IoT  IoT
IoT  IoT
IoT  IoT
IoT  IoT
IoT  IoT
IoT  IoT
IoT  IoT
IoT  IoT
IoT  IoT
IoT  IoT
IoT  物理学
物理学  雑記記事
雑記記事  IoT
IoT